Czy śmierć motyla w Amazonii może wywołać tornado w Polsce? Teoretycznie jest to możliwe! Matematycy udowadniają, że nawet mała zmiana warunków początkowych może doprowadzić do wielkich i całkowicie nieprzewidywalnych skutków. Efekt motyla to anegdotyczny przykład chaosu deterministycznego, który analizują także naukowcy z Wydziału Matematyki Stosowanej. Grupa pod kierunkiem dr. hab. Jana Borońskiego, prof. AGH, bada tzw. dziwne atraktory, czyli obiekty o strukturze fraktala, pojawiające się w układach chaotycznych.
Początki teorii chaosu
Wyobraźmy sobie postać, która zna wszystkie stany cząstek w całym Wszechświecie i na tej podstawie może przewidzieć jego przyszłość. Ten eksperyment myślowy, znany pod nazwą demona Laplace’a, obrazuje stanowisko determinizmu fizycznego głoszącego, że w świecie nie ma miejsca na przypadek. Istnienie takiej istoty wyklucza jednak mechanika kwantowa – zgodnie z zasadą nieoznaczoności są takie pary wielkości, których nie da się jednocześnie zmierzyć z dowolną dokładnością. Okazuje się przy tym, że przewidywanie przyszłości jest bardzo problematyczne także w mechanice klasycznej, natomiast element losowości może się pojawić nawet wtedy, kiedy znamy precyzyjnie stan danego układu.
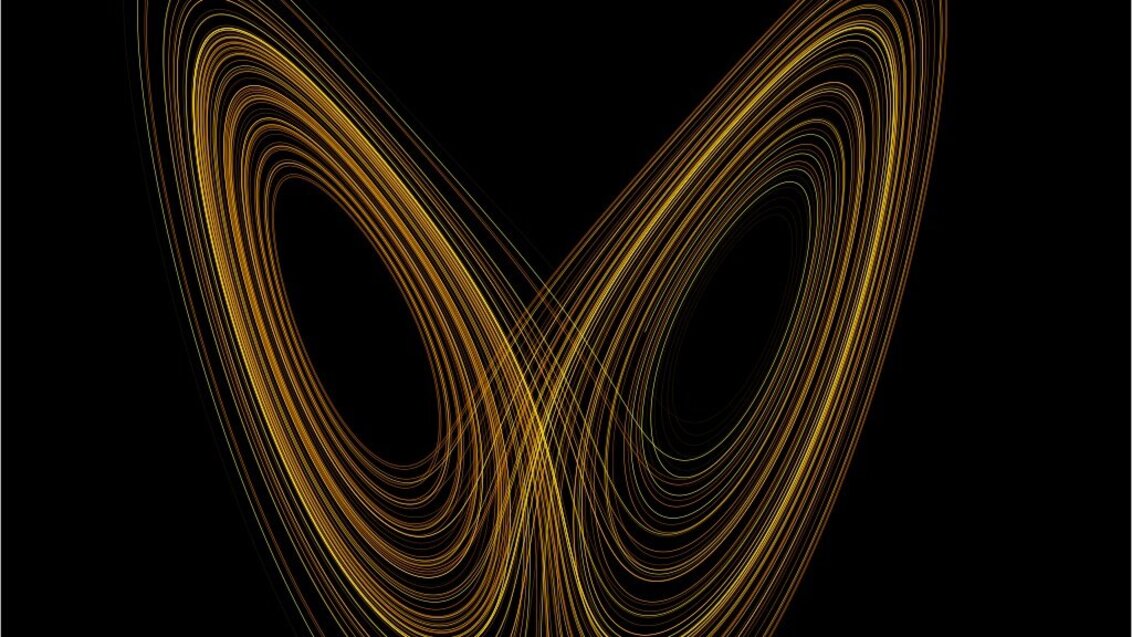
Atraktor Lorenza przypominający skrzydła motyla; źródło: Wikipedia
Jako pierwszy zauważył to Edward Lorenz, który badał zjawisko konwekcji. Odkrył on, że minimalne zaburzenie warunków początkowych może doprowadzić do nieproporcjonalnie wielkich zmian po pewnym czasie. Wyjaśnia to, dlaczego prognozowanie pogody jest do dzisiaj tak trudnym zajęciem – nawet ruch powietrza wywołany skrzydłami owada może urosnąć do huraganu, co popularnie nazywa się efektem motyla. Prace amerykańskiego naukowca poświęcone temu zagadnieniu zapoczątkowały zupełnie nową gałąź wiedzy, znaną jako teoria chaosu, którą zajmują się matematycy z WMS. Badają oni obiekty geometryczne zwane atraktorami chaotycznymi, do których należy też atraktor Lorenza.
Matematyczne przygody
Prof. Boroński uzyskał doktorat w Stanach Zjednoczonych u prof. Krystyny Kuperberg, znanej amerykańskiej matematyczki polskiego pochodzenia, która studiowała pod okiem przedstawicieli Warszawskiej Szkoły Matematycznej. Podczas pobytu badacz miał okazję poznać Jamesa Yorka, pioniera teorii chaosu, który został sportretowany jako matematyk w filmie Park Jurajski, gdzie pojawia się zresztą wątek związany z efektem motyla. Po powrocie z USA prof. Boroński kontynuował swoje badania nad atraktorami chaotycznymi, czego wynikiem była m.in. praca habilitacyjna dotycząca metody granic odwrotnych, za pomocą której można badać te skomplikowane obiekty matematyczne.
Matematyczne drzewo genealogiczne prof. Jana Borońskiego (obraz w pełnym rozmiarze)
Obecnie naukowiec w ramach projektu finansowanego przez NCN SONATA BIS kieruje zespołem naukowym, który zajmuje się parametrycznymi rodzinami atraktorów płaskich. Atraktor Hénona, należący do jednej z takich właśnie rodzin, stanowi – mówiąc w skrócie – dwuwymiarowe uproszczenie trójwymiarowego atraktora Lorenza. Prof. Boroński wraz ze współpracownikami próbuje iść jeszcze krok dalej i sprowadza w sposób izomorficzny dynamikę tych obiektów do dynamiki jednowymiarowych grafów topologicznych, a także dendrytów i ich ciągłych przekształceń. W ramach projektu badane są również bifurkacje, a więc np. skokowe przejścia od stanu prostego do złożonego atraktorów w zależności od parametru. Jednym z głównych zagadnień, nad którym pracuje zespół jest też problem postawiony przez prof. Yorka pod koniec lat 80-tych, dotyczący osiągalnej liczby obrotu atraktorów Hénona, który pozostaje nierozwiązany już od ponad trzech dekad.

 Jak uniknąć katastrofy w TUNELU? | Bunkier Nauki odc. 50
Jak uniknąć katastrofy w TUNELU? | Bunkier Nauki odc. 50  Jak nie dać się KLESZCZOM? | Bunkier Nauki odc. 49
Jak nie dać się KLESZCZOM? | Bunkier Nauki odc. 49  Jak podbijamy nanoświat – AGH NAUKA spotkania (nr 25)
Jak podbijamy nanoświat – AGH NAUKA spotkania (nr 25)  Jak samodzielnie wynieść 1000 worków śmieci z lasów? | Bunkier Nauki odc. 48
Jak samodzielnie wynieść 1000 worków śmieci z lasów? | Bunkier Nauki odc. 48  Obalamy MITY na temat sieci 5G – czy jest się czego bać? | Bunkier Nauki odc. 47
Obalamy MITY na temat sieci 5G – czy jest się czego bać? | Bunkier Nauki odc. 47  Ponad pół miliona zł na wsparcie kół naukowych AGH
Ponad pół miliona zł na wsparcie kół naukowych AGH  Wakacyjny pobyt ukraińskich dzieci w Łukęcinie. Apel do społeczności akademickiej AGH
Wakacyjny pobyt ukraińskich dzieci w Łukęcinie. Apel do społeczności akademickiej AGH  Spotkanie środowiska akademickiego Małopolski z Ministrem Nauki
Spotkanie środowiska akademickiego Małopolski z Ministrem Nauki